Заметки по символьным таблицам в Java 8

Заметки по символьным таблицам в Java 8

Символьная таблица, она же ассоциативный массив - суть то же, что и Map в Java, т.е. коллекция, где опеределенному ключу соответствует какое-то значение. При этом ключи взаимоисключающие, а значения нет.
В Java 8 предусмотрены 2 основные реализации, принципиально отличающиеся по принципу действия: TreeMap и  HashMap. Первая из них имеет временную сложность доступа O(log N), но гарантированную. Вторая O(1), но в среднем и при определенных условиях.

TreeMap

TreeMap является бинарным деревом, т.е. она разбита на ноды, для каждого из которых слева расположен нод с меньшим значением ключа (либо null), а справа нод с большим (либо null). Такое строение накладывает ограничения на ключи - они должны быть Comparable. При всем при этом TreeMap не просто бинарное дерево, а так называемое сбалансированное 2-3-4 черно-красное дерево. 

Сбалансированность здесь означает, что глубина дерева при структурных изменениях (добавление и удаление нодов) изменяется равномерно и будет равна во всех ветках дерева. Этим объсняется гарантированная временная сложность - до каждого листового нода добраться будет стоить log N, где бы он ни находился. Достигается такой баланс перестройкой дерева по мере изменения его структуры.

Структура дерева

Название 2-3-4 дерево означает, что это дерево на логическом уровне представляет собой иерархичный набор нодов, которые имеют соответственно 2, 3 или 4 дочерних нода, которые упорядочены между собой от большего к меньшему.

Логическое представление 2-3-4 дерева

Необходимо различать логическое представление дерева и его физическую реализацию. Прямая реализация с хранением ссылок на N дочерних элементов невыгодна и сложна в работе с ней - усложняются структурные преобразования, усложняется поиск. Поэтому пошли на компромис - оставили фактическую структуру дерева как бинарное с некоторой дополнительной информацией, а требования по балансу распространили только на логический уровень. Таким образом нод с 2-мя дочерними элементами - это по факту обычный бинарный нод и на физическом уровне он ничем не отличается от своего логического аналога. Остальные сложные ноды  составлены из набора бинарных нод, для которых используется специальный вид связи, обозначаемой красным цветом. Цвет связи храниться в дочернем ноде, т.к. связь с родителем (оно же ребро в графе/дереве) только одна и так выходит экономнее.

Физическое представление 2-3-4 дерева

Стоит отметить, что ситуация, когда у нода на физическом уровне может быть только один дочерний элемент справа или слева, может быть только у 3-нода на логческом уровне, то есть связь между ними обязательно будет красной.
Нод в дереве на физическом уровне имеет следующий вид:

static final class Entry implements Map.Entry {
    K key; 
    V value;
    Entry<K,V> left;       //потомок, который меньше
    Entry<K,V> right;      //потомок, который больше
    Entry<K,V> parent;     //родительский элемент - может быть как меньше, так и больше
    boolean color = BLACK; //цвет свзяи с родительским элементом
...
}

Поиск

Поиск по элемента по ключу является стандартным бинарным поиском. То есть если текущий элемент равен требуемому ключу, то это искомый элемент; если меньше, то поиск идет в левый дочерний нод; иначе в правый.

Добавление значения

Для вставки аналогично поиску ищется листовой элемент, к которому слева или справа в зависимости от сравнения, будет добавлен  новый нод. Связь между этими нодами отмечается красным и производится проверка был ли нарушен баланс в дереве. Для этого от этого нода до корня проводится проверка окружающих связей. Если обнаружится, что баланс нарушен, то производится перестроение дерева. Для этих целей используется ряд основных операций изменения структуры: инверсия, поворот влево и поворот вправо.

Поворот вправо

Поворот влево

Инверсия

Цвета связей на рисунках приведены для примера того, каким образом они сохраняются и  изменяются для нодов при операциях.

Удаление элемента

Для удаления элемента в общем случае он ищется в дереве, затем находится следующий листовой элемент, больший найденного (т.е. в правой ветке от него), значения меняются местами и листовой элемент удаляется из дерева. При этом, так же как и при добавлении, от листового элемента до рута производится проверка баланса и перестроение при необходимости. Для этого используют такие же операции изменения структуры.

Свойства TreeMap

Из-за  своей структуры бинарное дерево имеет некоторые интересные свойства. В первую очередь при правильном обходе дерева она является упорядоченной, т.е. элементы в ней отсортированы по ключу. Это свойство открывает целый ряд операций (не все из них представлены в TreeMap) таких как:

• поиск значений из выбранного диапазона [от; до], 
• наименьшее значение, которое больше или равно заданному (ceil)
• наибольшее значение, которое меньше или равно заданному (floor)
• ранговые операции (получение rank, поиск по rank, а не по ключу) - отсутствует в TreeMap
• минимальное и максимальное значения по ключу

У структуры бинарного дерева в целом есть не вполне очевидные особенности реализации, на которые опирается TreeMap в своей работе.

• Для получения минимального/максимального нода для определенного рута (не обязательно это рут всего дерева) необходимо идти все время влево/вправо, пока слева/справа не окажется null.
• Для получения следующего по порядку элемента для заданного нода возможны 2 ситуации:

1. у нода есть дочерний элемент справа - следующий элемент это минимум этой правой ветки
2. иначе необходимо итерироваться вверх по нодам и остановиться на том ноде, к которому пришли из левой ссылки. Этот нод и будет следующим. Если такого нет, то следующий нод отсутствует.

2-3 дерево

В целом, 2-3-4 дерево, коим является TreeMap, является частным случаем N-мерного дерева, т.е. дерева, в котором в узле может быть до N дочерних элементов. Существует вариант, называемый 2-3 черно-красное левостороннее дерево. В таком варианте помимо обычного 2-нода существует 3-нод, который на физическом уровне представляет собой композицию 2 нод с красной связью, причем такая связь должна вести только к левому дочернему ноду (именно поэтому оно левосторонее).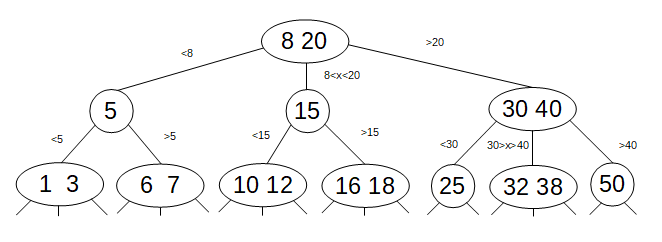

Логическое представление 2-3 дерева

Физическое представление 2-3 дерева

2-3 дерево в отличие от 2-3-4 имеет более строгий порядок, что ведет с одной стороны к более частым перестроениям, но с другой сохраняется больший баланс на физическом уровне. То есть в той ситуации, когда для 2-3-4 дерева наблюдается некоторый перекос в одну сторону, 2-3 дерево выглядит более равномерным.

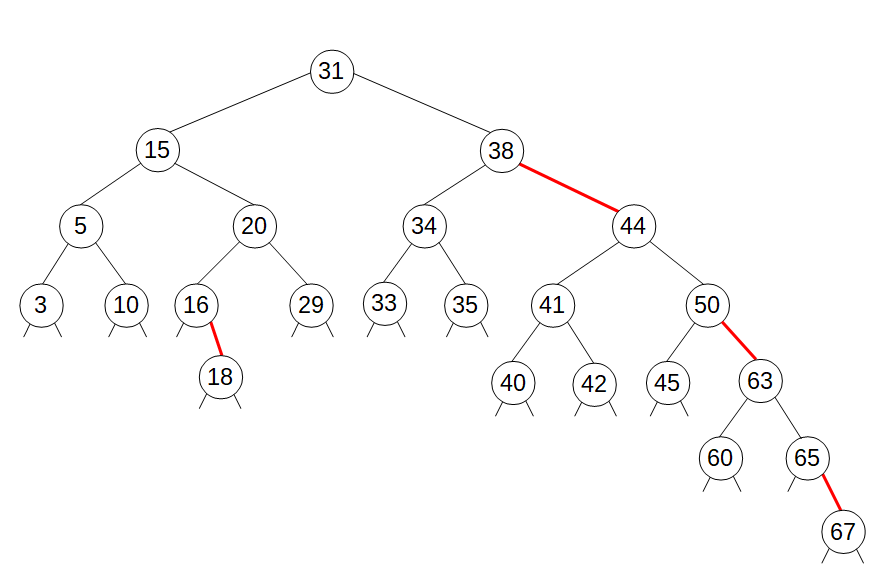Пример 2-3-4 дерева

Пример 2-3 дерева

 Тем не менее 2-3-4 дерево проще в реализации, в том числе из-за отсутствия необходимости соблюдения левосторонней ориентации.

 HashMap

HashMap в своей основе имеет стандартный массив элементов. Именно за счет этого достигается близкая к константе временная сложность. Позиция в массиве определяется специальной функцией hashCode, которая берется по модулю размера массива (capacity). Из-за ограниченной длины массива во время работы может возникнуть ситуация, когда для различных ключей и соответственно различных хеш-кодов позиция в массиве совпадет. Такое совпадение называется коллизией. Для того, чтобы корректно обрабатывать такую ситуацию, HashMap хранит в ячейках массива не просто пару ключ-значение, а связный список таких пар. При возникновении коллизии, если в имеющемся связном списке нет эквивалентного значения (проверяются хеш-коды и equals друг другу), то новое значение добавляется в этот список.

Нод в HashMap имеет такую структуру:

static class Node implements Map.Entry {
    final int hash;
    final K key;
    V value;
    Node next;
...
}

При поиске/удалении определяется ячейка по хеш-коду и производится перебор значений в списке, сравнивая хеш-код вместе с проверкой equals.

Схематичное изображение HashMap

Такая схема является реализацией одного из подходов к обработке коллизий в хеш-таблице - Separate Chaining Hash Table. Существует так же другой подход: Linear Probing Hash Table. Он заключется в том, что вместо хранения связного списка, значение при коллизии записывается в следующую по порядку свободную ячейку. Такой подход оправдан, если существуют ограничения по памяти.

Изменение размера

При увеличении количества элементов в HashMap увеличивается и количество коллизий. Чтобы избежать этого, при превышении общего количества элементов выше опеределенного порога, производится увеличение размера массива и перераспределение нодов по новому массиву. Порог может быть отрегулирован заданием параметра loadFactor при создании HashMap (по умолчанию это DEFAULT_LOAD_FACTOR = 0.75f). Изменение размера так же производится в том случае, если количество элементов в одном из связных списков становится слишком большим - больше 8 (но только если общее количество меньше 64 - об этом будет сказано дальше).
Размер массива всегда выбирается равным степени 2. Даже при явном указании размера при создании подбирается ближайшая степень, включающая заданное число. Такое поведение не случайно и имеет непосредственное влияние на процесс проведения перехеширования при изменении размера. Дело в том, что операция взятия по модулю для степени двойки представляется побитовым И с маской:  hashCode & (capacity - 1). Поэтому при увеличении размера в 2 раза разница в позиции со старым размером и новым будет всего в 1 бите, который совпадает со значением старой capacity.
Используя это свойство в HashMap, вместо перебора нод из связного списка и добавлении их в новую версию мапы, список делится на 2 части - те, которые соответствуют биту 0 в позиции старой capacity, остаются на месте, а те, у кторых 1, отправляются в ячейку со смещением в старую capacity от текущей (это будет новый выделенный участок массива).

Демонстрация разницы в 1 бит при изменени размера HashMap

В заключение темы с изменением размера HashMap можно отметить, что  обратного урезания capacity при уменьшении количества элементов не производится.

TreeNode

Связный список далек от производительного решения для хранения набора нодов. При значительном количестве коллизий изменение размера не дает значительного эффекта. В этом случае при превышении количества элементов в одной ячейке (TREEIFY_THRESHOLD = 8) и общего количества элементов (больше MIN_TREEIFY_CAPACITY = 64) связный список преобразуется в сбалансированное 2-3-4 черно-красное дерево. Т.е. в ячейках появляются небольшие копии аналога TreeMap.
Нод в этом случае имеет такой вид:

static final class TreeNode extends LinkedHashMap.Entry {
   // red-black tree links
   TreeNode parent;  
   TreeNode left;    //потомок, который меньше
   TreeNode right;   //потомок, который больше
   TreeNode prev;    // needed to unlink next upon deletion
   boolean red;      // цвет связи с родительским элементом
   //в наследство от LinkedHashMap.Entry
   Entry before, after;
   //в наследство от HashMap.Node
   final int hash;
   final K key;
   V value;
   Node next;
...
}

Как известно из предыдущего параграфа о TreeMap, для работы с бинарным деревом ключ должен быть Comparable. Для этого в  HashMap  используется в первую очередь хеш-код, но если он равен, то производится попытка определить является ли ключ Comparable и сравнить его помощью. Иначе просто ищется последовательно в обоих ветках относительно текущего нода. Таким образом, поиск элемента в ячейке массива сокращается до log N вместо N.
При вставке и удалении элементов дерева применяются аналогичные процедуры сохранения баланса, что и в TreeMap.

Во время увеличения capacity tree-ноды делятся на 2 дерева аналогичным образом как для обычного связного списка по 1 биту. Но при этом, если количество элементов в дереве будет меньше определенного порога (UNTREEIFY_THRESHOLD = 6), то дерево будет преобразовано обратно в связный список. Такое преобразование так же проводится при удалении элементов дерева, если его размер становится слишком малым.

Выбор реализации символьной таблицы

Обе описанные реализации достойные кандидаты на использование, имеющие те или иные преимущества и недостатки. В промышленной разработке в подавляющем большинстве случаев безоговорочно выбирается HashMap. Оно и понятно - константная временная сложность и что еще нужно для счастья?
Однако не все так однозначно. Успех применения хеш-таблицы всецело определяется качеством распределения хеш-кода. В идеале он должен иметь нормальное распределение, но это не всегда выполнимо и за этим практически никто не следит. Плохая реализация хеш-кода ведет к большому количеству коллизий, что вырождает HashMap в набор TreeMap. Вдобавок нельзя сбрасывать со счетов изменение размера capacity, что при вставке приводит к O(N). Для нивелирования этого, если заранее известен примерный размер таблицы, можно проставить capacity при создании HashMap, но в этом случае может быть выделено гораздо больше памяти, чем того требуется.
С другой стороны, в помощь разработчику существуют алгоритмы генерации нормального хеш-кода и любая IDE умеет генерировать такой хеш-код. Так же существуют библиотеки, которые берут заботу об этом на себя (к примеру lombok). Поэтому применения HashMap для большинства задач является оправданным, учитывая ее производительность. Вдобавок не всегда ключ может быть Comparable и для HashMap это не проблема.
В свою очередь, у TreeMap есть качество, которого нет у HashMap - порядок элементов. По своей сути TreeMap является аналогом индекса в БД. И для таких задач, где могут понадобиться выборки по диапазону значений или просто нужен порядок элементов по ключу, это кандидат номер 1. Это могут быть помимо простых выборок сложные геометрические задачи кластеризации, определения ближайшой точки, определение попадающих точек в определенную область и другие.